中仿科技社区中心

Moore’s Law for Solvers



News         | Posted on September 12th, 2012 by David Kan

At the heart of any simulation software are the solvers. Those are things that take geometry/mesh/physics to the computational results. While it’s convenient to think about solvers in terms of the type of study (think time-dependent, parametric, or eigenvalue), there is a hierarchy of solvers that are usually employed. And at the foundational level of any simulation — and for every iteration — there is a linear solver.



There are several types of linear solvers, but I won’t go into that now. (Maybe later if there’s enough demand.) Instead, I want to point out a little-known fact: linear solvers have improved at the same rate (or better) than hardware. Or put another way, Moore’s law holds for solver algorithms, too.

Most are familiar with Moore’s law, which states that “computer power doubles every two years”. Most associate this with hardware, whether it’s transistors on a chip or their speed. But back in 2005, the U.S. President’s Information Technology Advisory Committee (PITAC) issued a report that showed how solver algorithms have improved just as quickly.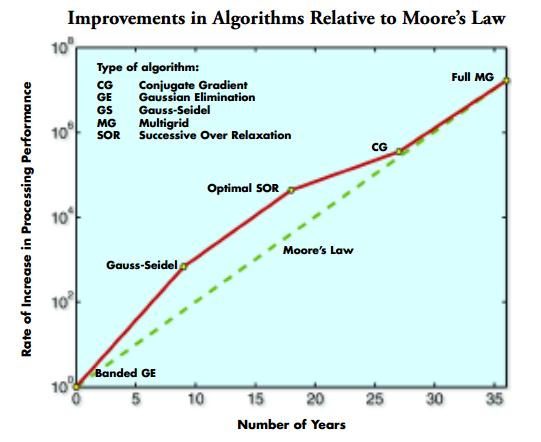



We featured this graph in the COMSOL Product Booklet some years ago because such information really matters. There is a significant amount of intellectual capital invested in this technology, and it’s good to be recognized. Just as pertinently, these solver algorithms are some of the very same ones you’ll find in COMSOL Multiphysics.

If anyone knows of an updated graph (this one is 7 years old), please share it with us in the comments below.